Kasıtlı ya da Değil: Tasarımda Matematiksel Teori
İlkelerden bazıları yüzlerce yaşında olabilir, ancak bugün hala iyi bir tasarıma sahipler. Zamanla test edilen matematiksel teoriler, neyin iyi göründüğüne dair kolektif tanımımızı uzun şekillendirdi.
Bazı matematiksel teorileri tasarım projenizin bir parçası olarak erken aşamalarda kullanmayı planlayabilirsiniz, diğerleri istenmeden olabilir. Her iki durumda da matematiksel kurallar, baskıdan web tasarımına kadar neredeyse her proje için geçerlidir. Matematiğin tasarımdaki rolünü anlamak ve projelerinizin görünümünü ve hissini nasıl etkileyebileceğini açıklamak önemlidir.
Makaleyi beğendiniz mi? RSS beslememize abone olmayı ve son içeriklerden haberdar olmak için bizi Twitter'da takip etmeyi unutmayın.
Altın Oran


Altın dikdörtgen veya altın ortalama olarak da adlandırılan altın oran, 1 ila 1.618 arasında bir şekle sahiptir. (Bu sayı, 1.618… genellikle Phi olarak adlandırılır.) Teorinin kesin kökenleri bilinmemektedir, ancak altın oranın her yerde olduğu belirtilmektedir - Eqypt'teki Büyük Piramitlerden Yunanistan'daki Parthenon'un şekline kadar.
Ancak şekil mimari ile sınırlı değildir. Ünlü sanat eserlerinde (Leonardo Da Vinci'nin “Vitruvius Adamı”) ve hatta mevcut web tasarımında (daha yeni Twitter site tasarımı) bulunabilir.
Basılı ve web tasarım projeleri için başvurular bu orandan 1.618'e oranla biraz daha az keskindir, ancak yine de teori ile uyumludur. (Birçok tasarımcı, çalışmak daha kolay numaralar veya ızgaralar oluşturmak için altın rasyonla çalışırken sayıları yuvarlar.)
Altın oranı birkaç farklı şekilde kullanabilirsiniz - genel siteniz veya tasarımınızın farklı bölümleri için anahat olarak. Altın oranın en iyi kısımlarından biri? Oranı kullanarak parçaları grupladığınızda, son şekliniz de oranı yansıtacaktır, çünkü şekil sonsuz (ve mükemmel) şekilde kendine bölünebilir.
Peki altın oran ne yapar? Basitçe, denge ve uyum duygusu yaratırken doğanın görünümünü taklit eder.
Fibonacci Dizisi


Fibonacci dizisi, listedeki her sayının önceki iki sayının eklenmesinden türetildiği bir sayı dizisidir.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811…
Matematik teorisi 750 yıldan fazladır ve Leonardo Pisano Bogollo tarafından İtalya'da geliştirilmiştir. Takma adı “Fibonacci” idi ve aynı zamanda mevcut sayı sistemimizin kullanım ömrü boyunca Avrupa'ya yayılmasına yardımcı oldu (1170-1250).
Bu sayı dizisinin sonucu olarak, her halkanın bu oran ile önceki ile ilişkili olduğu spiral bir şekildir. Doğada bunun en yaygın örneği nautilus'tur.
Tasarım uygulamaları için, sekanstan bloklar bir araya getirildiğinde bir kare sarmal oluşturur. Ayrıca bu teori altın orana bağlanır - Fibonacci dizisinde birbirini takip eden iki sayıyı bir araya getirirseniz, oran 1 ila 1.1618 ile çok yakından ilgilidir. Sayılar büyüdükçe Phi ile daha yakın olurlar.
Yine, bu teori tasarımda denge ve uyum yaratmak için harika ve oluşturulması oldukça kolay olabilir. Genellikle tasarımcıların web sitelerinde gövde ve kenar çubukları için genişlikleri ve boyutlandırmayı belirlemelerine yardımcı olmak için kullanılır ve en çok bloglar ve dergi tarzı düzenlerle çalışırken kullanılır. Fibonacci dizisini kullanan üç sütun düzeninde, örneğin 1.170 piksel genişliğinde bir düzende sütunlar 180, 270 ve 720 piksel genişliğindedir.
Üçte Bir Kuralı


Üçte bir kuralı, kaçınamayacağınız matematiksel teorilerden biridir. Basılı veya dijital olarak yayınlanan her işte görünecektir.
Basitçe, üçte bir kural, dokuz dikdörtgenin her birinin aynı boyutta olduğu herhangi bir şekil veya boyuttaki herhangi bir görüntünün (veya tasarımın) üstüne uyan 3'e 3 hayali bir ızgaradır. Teori, tasarımcıların (ve fotoğrafçıların) gözün tek bir görüntüyü veya bir görüntü grubunu (web sitesi gibi) nasıl takip ettiğini belirlemesine yardımcı olur.
Fotoğraflar için ekinlerin belirlenmesine ve görüntülerin gruplara yerleştirilmesine yardımcı olmak için üçte bir kuralı kullanın. Teoriye göre, göz ilk önce sol üst kavşakta durur, sonra aşağı doğru hareket eder, sonra sağ üst kavşağa ve daha sonra tekrar aşağı doğru hareket eder. (Bu yüzden çoğu tasarımda sol üstte logolar ve iletişim bilgileri bulunur.)
Üçte bir kuralı, tasarımda bir denge duygusu yaratmanıza yardımcı olan başka bir araçtır. Yol boyunca şaşırtıcı bulabileceğiniz şey, bu dengenin genellikle asimetrik olmasıdır. Göz, bu dokuz bloklu ızgaradaki kavşaklar boyunca düştüğü için, merkez referans noktası yoktur.
Bu Design Shack makalesinde üçte üçü ve üçlü grupları kullanma hakkında daha fazla bilgi edinin.
kundli


Bir insan Hint kültüründe doğduğunda gezegenlerin konumunu tanımlayan Kundli'nin astrolojik teorisi, beş elementli bir tasarım şeması oluşturur.
Kundli'nin ana hatlarını kullanarak dört küçük kare içeren bir kareden başlayarak bir tasarım oluşturun. Tasarım öğeleri, daha az belirgin bir uyum tarzı oluşturmak için bu karelerin caddy köşeli şekline göre yerleştirilir.
Kundli'yi ayrıca, üç köşeden üçte imge ve metnin bulunmadığı üçte bir kuralın bir uzantısı olarak da düşünebilirsiniz.
Kundli prensibi genellikle aynı şekil ve boyutta birden fazla görüntü ile çalışırken kullanılır. Tasarımcılara, her görüntüyü tek bir düzlemde sıralamaksızın gruplandırmalar oluşturmanın bir yolunu sunar.
Izgaralar

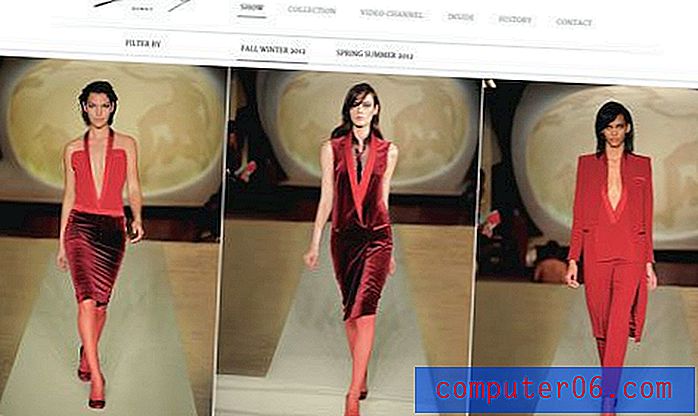
Tasarım taslağı oluşturmak için ızgaraları kullanmak, tasarımcılar için en yaygın matematiksel araçlardan biridir. Nesne yerleşimini belirlemeye yardımcı olmak için bir belgede görünmez sütunlar veya satırlar ayarlayarak, belirgin bir düzen duygusu yaratmaya yardımcı olursunuz.
En iyi ızgaralar, bir dizi sütun (veya satır) ve eşit artışlara sahip oluklar kullanılarak oluşturulur. Farklı projeler farklı ızgara yapıları gerektirir. Örneğin gazeteler baskı tasarımlarını genellikle altı sütunlu bir ızgara yapısına dayandırırlar; web sitesi ızgaraları daha geniş çapta değişiklik gösterir ve üç sütundan en az 16'ya kadar değişebilir.
Bir sütun ızgarası kullanmak, tüm öğelerin ızgaraya düştüğünden emin olmak için biraz matematik gerektirir. Ancak korkutmayın, bu satırlara sığacak şekilde kopya bloklarını ve görüntüleri ölçtüğünüzde sayıların yönetimi genellikle kolaydır.
Eğlenceli Matematiksel Tasarım Araçları
Matematik ile biraz eğlenin ama tasarlarken sayılarla boğuşmayın. Belirtilen bir çerçeveye göre boyutları ve spesifikasyonları anlamanıza yardımcı olabilecek birkaç araç.
Altın Oran Hesaplayıcı
Phi Hesap Makinesi
Altın Oran Tipografi Hesaplama
Fibonacci Dizi Hesaplayıcı
Izgara Hesaplayıcı
Sonuç
Matematiksel ilkeleri tasarımda kullanmak, bir organizasyon duygusu, denge ve genel olarak kolay göz hissi yaratmaya yardımcı olabilir. Bu teorilerin çoğu, sayılarla desteklenmiş olmalarına rağmen, doğada dayanır ve ima ettikleri ahenkli duygulara katkıda bulunur.
Projeler üzerinde çalışırken sayılara düşmeyin. Teorileri bilerek ve projenizle ilgili olup olmadığını anlayarak başlayın. Yaratıcılığınızın tasarımı yönlendirmesine ve içindeki ayrıntıları mükemmelleştirmek için bilimi kullanmasına izin verin.
Görüntü Kaynakları: GeometerArtist, theilr, Hitchster ve brklynn.